Torsion of a 3D cylinder#
Units#
Length: mm
Mass: kg
Time: s
Force: milliNewtons
Stress: kPa
Software:#
Dolfinx v0.8.0
In the collection “Example Codes for Coupled Theories in Solid Mechanics,”
By Eric M. Stewart, Shawn A. Chester, and Lallit Anand.
Import modules#
# Import FEnicSx/dolfinx
import dolfinx
# For numerical arrays
import numpy as np
# For MPI-based parallelization
from mpi4py import MPI
comm = MPI.COMM_WORLD
rank = comm.Get_rank()
# PETSc solvers
from petsc4py import PETSc
# specific functions from dolfinx modules
from dolfinx import fem, mesh, io, plot, log
from dolfinx.fem import (Constant, dirichletbc, Function, functionspace, Expression )
from dolfinx.fem.petsc import NonlinearProblem
from dolfinx.nls.petsc import NewtonSolver
from dolfinx.io import VTXWriter, XDMFFile
# specific functions from ufl modules
import ufl
from ufl import (TestFunctions, TrialFunction, Identity, grad, det, div, dev, inv, tr, sqrt, conditional ,\
gt, dx, inner, derivative, dot, ln, split)
# basix finite elements (necessary for dolfinx v0.8.0)
import basix
from basix.ufl import element, mixed_element, quadrature_element
# Matplotlib for plotting
import matplotlib.pyplot as plt
plt.close('all')
# For timing the code
from datetime import datetime
# Set level of detail for log messages (integer)
# Guide:
# CRITICAL = 50, // errors that may lead to data corruption
# ERROR = 40, // things that HAVE gone wrong
# WARNING = 30, // things that MAY go wrong later
# INFO = 20, // information of general interest (includes solver info)
# PROGRESS = 16, // what's happening (broadly)
# TRACE = 13, // what's happening (in detail)
# DBG = 10 // sundry
#
log.set_log_level(log.LogLevel.WARNING)
Define geometry#
L = 25.4 # Length mm
R = 12.7 # Radius mm
with XDMFFile(MPI.COMM_WORLD,"meshes/cylinder.xdmf",'r') as infile:
domain = infile.read_mesh(name="Grid",xpath="/Xdmf/Domain")
cell_tags = infile.read_meshtags(domain,name="Grid")
domain.topology.create_connectivity(domain.topology.dim, domain.topology.dim-1)
with XDMFFile(MPI.COMM_WORLD, "meshes/facet_cylinder.xdmf", "r") as xdmf:
facet_tags = xdmf.read_meshtags(domain, name="Grid")
x = ufl.SpatialCoordinate(domain)
Print out the unique facet index numbers
top_imap = domain.topology.index_map(2) # index map of 2D entities in domain (facets)
values = np.zeros(top_imap.size_global) # an array of zeros of the same size as number of 2D entities
values[facet_tags.indices]=facet_tags.values # populating the array with facet tag index numbers
print(np.unique(facet_tags.values)) # printing the unique indices
# Surface labels from gmsh:
# Physical Surface("xBot", 101)
# Physical Surface("xTop", 102)
# The "side" is automatically assigned index 7.
[ 7 101 102]
Visualize reference configuration and boundary facets
import pyvista
pyvista.set_jupyter_backend('html')
from dolfinx.plot import vtk_mesh
pyvista.start_xvfb()
plotter = pyvista.Plotter()
top = pyvista.UnstructuredGrid(*vtk_mesh(domain, domain.topology.dim-1,facet_tags.indices[facet_tags.values==102]) )
sides = pyvista.UnstructuredGrid(*vtk_mesh(domain, domain.topology.dim-1,facet_tags.indices[facet_tags.values==7]) )
bottom = pyvista.UnstructuredGrid(*vtk_mesh(domain, domain.topology.dim-1,facet_tags.indices[facet_tags.values==101]) )
actor = plotter.add_mesh(top, show_edges=True,color="blue") # top face is blue
actor2 = plotter.add_mesh(sides, show_edges=True,color="red") # sides are red
actor3 = plotter.add_mesh(bottom, show_edges=True,color="green") # bottom face is green
labels = dict(zlabel='Z', xlabel='X', ylabel='Y')
plotter.add_axes(**labels)
plotter.screenshot("mesh.png")
from IPython.display import Image
Image(filename='mesh.png')

Define boundary and volume integration measure#
# Surface labels from gmsh:
# Physical Surface("xBot", 101)
# Physical Surface("xTop", 102)
# Define the boundary integration measure "ds" using the facet tags,
# also specify the number of surface quadrature points.
ds = ufl.Measure('ds', domain=domain, subdomain_data=facet_tags, metadata={'quadrature_degree': 4})
# Define the volume integration measure "dx"
# also specify the number of volume quadrature points.
dx = ufl.Measure('dx', domain=domain, metadata={'quadrature_degree': 4})
# Define facet normal
n = ufl.FacetNormal(domain)
Material parameters#
-Arruda-Boyce model
Gshear_0 = Constant(domain,PETSc.ScalarType(280.0)) # Ground state shear modulus
lambdaL = Constant(domain,PETSc.ScalarType(5.12)) # Locking stretch
Kbulk = Constant(domain,PETSc.ScalarType(1000.0*Gshear_0))
Function spaces#
# dolfinx v0.8.0 syntax:
U2 = element("Lagrange", domain.basix_cell(), 2, shape=(3,)) # For displacement
P1 = element("Lagrange", domain.basix_cell(), 1) # For pressure
#
TH = mixed_element([U2, P1]) # Taylor-Hood style mixed element
ME = functionspace(domain, TH) # Total space for all DOFs
# Define actual functions with the required DOFs
w = Function(ME)
u, p = split(w) # displacement u, pressure p
# A copy of functions to store values in the previous step
w_old = Function(ME)
u_old, p_old = split(w_old)
# Define test functions
u_test, p_test = TestFunctions(ME)
# Define trial functions needed for automatic differentiation
dw = TrialFunction(ME)
Initial conditions#
The initial conditions for degrees of freedom u and p are zero everywhere
These are imposed automatically, since we have not specified any non-zero initial conditions.
Subroutines for kinematics and constitutive equations#
# Deformation gradient
def F_calc(u):
Id = Identity(3)
F = Id + grad(u)
return F
def lambdaBar_calc(u):
F = F_calc(u)
C = F.T*F
Cdis = J**(-2/3)*C
I1 = tr(Cdis)
lambdaBar = sqrt(I1/3.0)
return lambdaBar
def zeta_calc(u):
lambdaBar = lambdaBar_calc(u)
# Use Pade approximation of Langevin inverse
z = lambdaBar/lambdaL
z = conditional(gt(z,0.95), 0.95, z) # Keep simulation from blowing up
beta = z*(3.0 - z**2.0)/(1.0 - z**2.0)
zeta = (lambdaL/(3*lambdaBar))*beta
return zeta
# Generalized shear modulus for Arruda-Boyce model
def Gshear_AB_calc(u):
zeta = zeta_calc(u)
Gshear = Gshear_0 * zeta
return Gshear
#---------------------------------------------
# Subroutine for calculating the Cauchy stress
#---------------------------------------------
def T_calc(u,p):
Id = Identity(3)
F = F_calc(u)
J = det(F)
B = F*F.T
Bdis = J**(-2/3)*B
Gshear = Gshear_AB_calc(u)
T = (1/J)* Gshear * dev(Bdis) - p * Id
return T
#----------------------------------------------
# Subroutine for calculating the Piola stress
#----------------------------------------------
def Piola_calc(u, p):
Id = Identity(3)
F = F_calc(u)
J = det(F)
#
T = T_calc(u,p)
#
Tmat = J * T * inv(F.T)
return Tmat
Evaluate kinematics and constitutive relations#
F = F_calc(u)
J = det(F)
lambdaBar = lambdaBar_calc(u)
# Piola stress
Tmat = Piola_calc(u, p)
Weak forms#
# Residuals:
# Res_0: Balance of forces (test fxn: u)
# Res_1: Coupling pressure (test fxn: p)
# The weak form for the equilibrium equation. No body force
Res_0 = inner(Tmat , grad(u_test) )*dx
# The weak form for the pressure
fac_p = ln(J)/J
#
Res_1 = dot( (p/Kbulk + fac_p), p_test)*dx
# Total weak form
Res = Res_0 + Res_1
# Automatic differentiation tangent:
a = derivative(Res, w, dw)
Set-up output files#
# results file name
results_name = "3D_torsion"
# v0.8.0 syntax:
U1 = element("DG", domain.basix_cell(), 1, shape=(3,)) # For displacement
P0 = element("DG", domain.basix_cell(), 1) # For pressure
V2 = fem.functionspace(domain, U1) #Vector function space
V1 = fem.functionspace(domain, P0) #Scalar function space, must be discontinuous here since materials are discontinuous.
# fields to write to output file
u_vis = Function(V2)
u_vis.name = "disp"
p_vis = Function(V1)
p_vis.name = "p"
J_vis = Function(V1)
J_vis.name = "J"
J_expr = Expression(J,V1.element.interpolation_points())
lambdaBar_vis = Function(V1)
lambdaBar_vis.name = "lambdaBar"
lambdaBar_expr = Expression(lambdaBar,V1.element.interpolation_points())
P11 = Function(V1)
P11.name = "P11"
P11_expr = Expression(Tmat[0,0],V1.element.interpolation_points())
P22 = Function(V1)
P22.name = "P22"
P22_expr = Expression(Tmat[1,1],V1.element.interpolation_points())
P33 = Function(V1)
P33.name = "P33"
P33_expr = Expression(Tmat[2,2],V1.element.interpolation_points())
T = Tmat*F.T/J
T0 = T - (1/3)*tr(T)*Identity(3)
Mises = sqrt((3/2)*inner(T0, T0))
Mises_vis= Function(V1,name="Mises")
Mises_expr = Expression(Mises,V1.element.interpolation_points())
# set up the output VTX files.
file_results = VTXWriter(
MPI.COMM_WORLD,
"results/" + results_name + ".bp",
[ # put the functions here you wish to write to output
u_vis, p_vis, J_vis, P11, P22, P33, lambdaBar_vis,
Mises_vis,
],
engine="BP4",
)
def writeResults(t):
# Output field interpolation
u_vis.interpolate(w.sub(0))
p_vis.interpolate(w.sub(1))
J_vis.interpolate(J_expr)
P11.interpolate(P11_expr)
P22.interpolate(P22_expr)
P33.interpolate(P33_expr)
lambdaBar_vis.interpolate(lambdaBar_expr)
Mises_vis.interpolate(Mises_expr)
# Write output fields
file_results.write(t)
Infrastructure for pulling out time history data (force, displacement, etc.)#
# infrastructure for evaluating functions at a certain point efficiently
# (not actually used in this code)
pointForStress = np.array([L, 0, 0])
bb_tree = dolfinx.geometry.bb_tree(domain,domain.topology.dim)
cell_candidates = dolfinx.geometry.compute_collisions_points(bb_tree, pointForStress)
colliding_cells = dolfinx.geometry.compute_colliding_cells(domain, cell_candidates, pointForStress).array
# Define functions (UFL forms) for evaluating the torque and normal traction on the top surface
origin = ufl.as_vector([0.0,0.0,0.0])
traction = dot(Tmat,n)
#
vec = ufl.cross((x-origin),traction)
Torque = fem.form(dot(vec,n)*ds(101))
#
Force = fem.form(dot(traction,n)*ds(101))
# Surface labels from gmsh:
# Physical Surface("xBot", 101)
# Physical Surface("xTop", 102)
Name the analysis step#
# Give the step a descriptive name
step = "Twist"
Boundary condtions#
# Setting up the expressions for rotation of the top surface.
scale = 1.0
y0 = 0.0
z0 = 0.0
Time_cons = Constant(domain,PETSc.ScalarType(0))
V_y, V_y_to_ME = ME.sub(0).sub(1).collapse() #Scalar function space corresponding to u2 / y-displacement
V_z, V_z_to_ME = ME.sub(0).sub(2).collapse() #Scalar function space corresponding to u3 / z-displacement
boundary_twist_y = scale*(y0 + (x[1] - y0)*ufl.cos(theta_tot*(Time_cons/Ttot)) - (x[2] - z0)*ufl.sin(theta_tot*(Time_cons/Ttot)) - x[1])
exp_y = Expression(boundary_twist_y,V_y.element.interpolation_points())
func_y = Function(V_y)
func_y.interpolate(exp_y)
boundary_twist_z = scale*(z0 + (x[1] - y0)*ufl.sin(theta_tot*(Time_cons/Ttot)) + (x[2] - z0)*ufl.cos(theta_tot*(Time_cons/Ttot)) - x[2])
exp_z = Expression(boundary_twist_z,V_z.element.interpolation_points())
func_z = Function(V_z)
func_z.interpolate(exp_z)
# Surface labels from gmsh:
# Physical Surface("xBot", 101)
# Physical Surface("xTop", 102)
# Find the specific DOFs which will be constrained.
#
# Bottom surface displacement degrees of freedom
Btm_dofs_u1 = fem.locate_dofs_topological(ME.sub(0).sub(0), facet_tags.dim, facet_tags.find(101))
Btm_dofs_u2 = fem.locate_dofs_topological(ME.sub(0).sub(1), facet_tags.dim, facet_tags.find(101))
Btm_dofs_u3 = fem.locate_dofs_topological(ME.sub(0).sub(2), facet_tags.dim, facet_tags.find(101))
# Top surface displacement degrees of freedom
Top_dofs_u1 = fem.locate_dofs_topological(ME.sub(0).sub(0), facet_tags.dim, facet_tags.find(102))
Top_dofs_u2 = fem.locate_dofs_topological((ME.sub(0).sub(1), V_y), facet_tags.dim, facet_tags.find(102))
Top_dofs_u3 = fem.locate_dofs_topological((ME.sub(0).sub(2), V_z), facet_tags.dim, facet_tags.find(102))
# Build the Dirichlet BCs
bcs_0 = dirichletbc(0.0, Btm_dofs_u1, ME.sub(0).sub(0)) # u1 fix - xBtm
bcs_1 = dirichletbc(0.0, Btm_dofs_u2, ME.sub(0).sub(1)) # u2 fix - xBtm
bcs_2 = dirichletbc(0.0, Btm_dofs_u3, ME.sub(0).sub(2)) # u3 fix - xBtm
#
bcs_3 = dirichletbc(0.0, Top_dofs_u1, ME.sub(0).sub(0)) # u1 fix - xTop
bcs_4 = dirichletbc(func_y, Top_dofs_u2, ME.sub(0).sub(1)) # u2 rotate - xTop
bcs_5 = dirichletbc(func_z, Top_dofs_u3, ME.sub(0).sub(2)) # u3 rotate - xTop
# collect all BCs in one object.
bcs = [bcs_0, bcs_1, bcs_2, bcs_3, bcs_4, bcs_5]
Define the nonlinear variational problem#
# # Optimization options for the form compiler
# Set up nonlinear problem
problem = NonlinearProblem(Res, w, bcs, a)
# the global newton solver and params
solver = NewtonSolver(MPI.COMM_WORLD, problem)
solver.convergence_criterion = "incremental"
solver.rtol = 1e-8
solver.atol = 1e-8
solver.max_it = 50
solver.report = True
# The Krylov solver parameters.
ksp = solver.krylov_solver
opts = PETSc.Options()
option_prefix = ksp.getOptionsPrefix()
opts[f"{option_prefix}ksp_type"] = "preonly"
opts[f"{option_prefix}pc_type"] = "lu" # do not use 'gamg' pre-conditioner
opts[f"{option_prefix}pc_factor_mat_solver_type"] = "mumps"
opts[f"{option_prefix}ksp_max_it"] = 30
ksp.setFromOptions()
Start calculation loop#
# Variables for storing time history
totSteps = numSteps+1
timeHist0 = np.zeros(shape=[totSteps])
timeHist1 = np.zeros(shape=[totSteps])
timeHist2 = np.zeros(shape=[totSteps])
#Iinitialize a counter for reporting data
ii=0
# Write initial state to file
writeResults(t=0.0)
# Print out message for simulation start
print("------------------------------------")
print("Simulation Start")
print("------------------------------------")
# Store start time
startTime = datetime.now()
# Time-stepping solution procedure loop
while (round(t + dt, 9) <= Ttot):
# increment time
t += dt
# increment counter
ii += 1
# update time variables in time-dependent BCs
Time_cons.value = t
func_y.interpolate(exp_y)
func_z.interpolate(exp_z)
# Solve the problem
try:
(iter, converged) = solver.solve(w)
except: # Break the loop if solver fails
print("Ended Early")
break
# Collect results from MPI ghost processes
w.x.scatter_forward()
# Write output to file
writeResults(t)
# Update DOFs for next step
w_old.x.array[:] = w.x.array
# Store time history variables at this time
timeHist0[ii] = theta_tot*(t/Ttot) # Current twist angle
timeHist1[ii] = domain.comm.gather(fem.assemble_scalar(Torque))[0] # time history of reaction torque
timeHist2[ii] = domain.comm.gather(fem.assemble_scalar(Force))[0] # time history of axial force
# Print progress of calculation
if ii%1 == 0:
now = datetime.now()
current_time = now.strftime("%H:%M:%S")
print("Step: {} | Increment: {}, Iterations: {}".\
format(step, ii, iter))
print(" Simulation Time: {} s of {} s".\
format(round(t,4), Ttot))
print()
# close the output file.
file_results.close()
# End analysis
print("-----------------------------------------")
print("End computation")
# Report elapsed real time for the analysis
endTime = datetime.now()
elapseTime = endTime - startTime
print("------------------------------------------")
print("Elapsed real time: {}".format(elapseTime))
print("------------------------------------------")
------------------------------------
Simulation Start
------------------------------------
Step: Twist | Increment: 1, Iterations: 5
Simulation Time: 1.0 s of 20 s
Step: Twist | Increment: 2, Iterations: 5
Simulation Time: 2.0 s of 20 s
Step: Twist | Increment: 3, Iterations: 5
Simulation Time: 3.0 s of 20 s
Step: Twist | Increment: 4, Iterations: 5
Simulation Time: 4.0 s of 20 s
Step: Twist | Increment: 5, Iterations: 5
Simulation Time: 5.0 s of 20 s
Step: Twist | Increment: 6, Iterations: 5
Simulation Time: 6.0 s of 20 s
Step: Twist | Increment: 7, Iterations: 5
Simulation Time: 7.0 s of 20 s
Step: Twist | Increment: 8, Iterations: 5
Simulation Time: 8.0 s of 20 s
Step: Twist | Increment: 9, Iterations: 5
Simulation Time: 9.0 s of 20 s
Step: Twist | Increment: 10, Iterations: 5
Simulation Time: 10.0 s of 20 s
Step: Twist | Increment: 11, Iterations: 5
Simulation Time: 11.0 s of 20 s
Step: Twist | Increment: 12, Iterations: 5
Simulation Time: 12.0 s of 20 s
Step: Twist | Increment: 13, Iterations: 5
Simulation Time: 13.0 s of 20 s
Step: Twist | Increment: 14, Iterations: 5
Simulation Time: 14.0 s of 20 s
Step: Twist | Increment: 15, Iterations: 5
Simulation Time: 15.0 s of 20 s
Step: Twist | Increment: 16, Iterations: 5
Simulation Time: 16.0 s of 20 s
Step: Twist | Increment: 17, Iterations: 5
Simulation Time: 17.0 s of 20 s
Step: Twist | Increment: 18, Iterations: 5
Simulation Time: 18.0 s of 20 s
Step: Twist | Increment: 19, Iterations: 5
Simulation Time: 19.0 s of 20 s
Step: Twist | Increment: 20, Iterations: 5
Simulation Time: 20.0 s of 20 s
-----------------------------------------
End computation
------------------------------------------
Elapsed real time: 0:02:18.379461
------------------------------------------
Plot results#
# set plot font to size 14
font = {'size' : 14}
plt.rc('font', **font)
# Get array of default plot colors
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
# Torque versus twist curve:
#
fig = plt.figure()
#fig.set_size_inches(7,4)
ax=fig.gca()
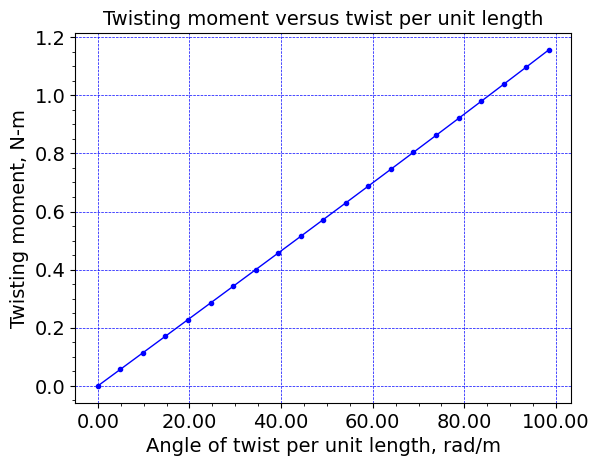
plt.plot(timeHist0/25.4E-3, timeHist1/1.E6 , c='b', linewidth=1.0, marker='.')
#-------------------------------------------------------------
#ax.set.xlim(-0.01,0.01)
#ax.set.ylim(-0.03,0.03)
#plt.axis('tight')
plt.grid(linestyle="--", linewidth=0.5, color='b')
ax.set_xlabel("Angle of twist per unit length, rad/m",size=14)
ax.set_ylabel("Twisting moment, N-m",size=14)
ax.set_title("Twisting moment versus twist per unit length", size=14, weight='normal')
from matplotlib.ticker import AutoMinorLocator,FormatStrFormatter
ax.xaxis.set_minor_locator(AutoMinorLocator())
ax.yaxis.set_minor_locator(AutoMinorLocator())
import matplotlib.ticker as ticker
ax.xaxis.set_major_formatter(ticker.FormatStrFormatter('%0.2f'))
plt.show()
fig = plt.gcf()
fig.set_size_inches(7,5)
plt.tight_layout()
plt.savefig("results/3D_torsion_torque_twist.png", dpi=600)
# Normal force versus twist curve:
#
fig = plt.figure()
#fig.set_size_inches(7,4)
ax=fig.gca()
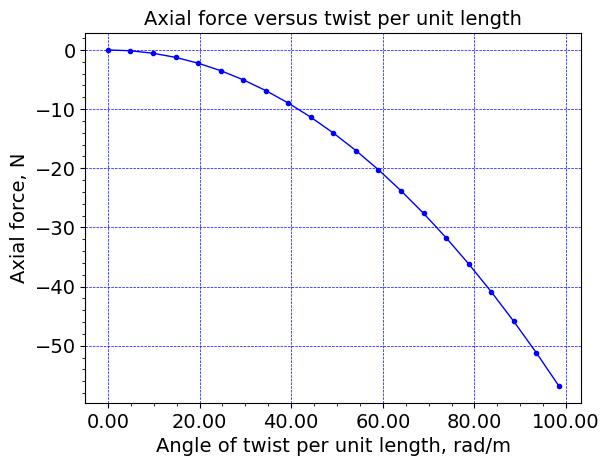
plt.plot(timeHist0/25.4E-3, timeHist2/1.E3, c='b', linewidth=1.0, marker='.')
#-------------------------------------------------------------
#ax.set.xlim(-0.01,0.01)
#ax.set.ylim(-0.03,0.03)
#plt.axis('tight')
plt.grid(linestyle="--", linewidth=0.5, color='b')
ax.set_xlabel("Angle of twist per unit length, rad/m",size=14)
ax.set_ylabel("Axial force, N",size=14)
ax.set_title("Axial force versus twist per unit length", size=14, weight='normal')
from matplotlib.ticker import AutoMinorLocator,FormatStrFormatter
ax.xaxis.set_minor_locator(AutoMinorLocator())
ax.yaxis.set_minor_locator(AutoMinorLocator())
import matplotlib.ticker as ticker
ax.xaxis.set_major_formatter(ticker.FormatStrFormatter('%0.2f'))
plt.show()
fig = plt.gcf()
fig.set_size_inches(7,5)
plt.tight_layout()
plt.savefig("results/3D_torsion_axial_force_twist.png", dpi=600)
<Figure size 700x500 with 0 Axes>
<Figure size 700x500 with 0 Axes>